
车身噪声传递函数分析
2010/7/7 16:53:00
1 引言
NVH性能是新车的重要性能指标之一。车身在整车的NVH性能中有着重要影响,不论是来自路面的激励,还是来自发动机的激励,都是通过车身传递给乘员。开发出合理的车身结构对提高整车的NVH性能有重要作用。车身噪声传递函数(NTF)分析就是车身开发中的重要方法之一。
将对车身与底盘之间的主要连接区域进行声学传递函数分析,以便找出噪音传递路径与对NVH特性影响比较大的关键零部件。分析时一个声学空腔模型将被包括在内并用来预测内噪声水平,车辆的详细有限元模型与声学空腔模型将被耦合并求解,通过车身与动力系统及底盘系统连接点上施加载荷来计算车内乘员耳侧的噪声响应。
2 分析模型
车身分析的有限元模型包括车身结构的有限元模型和车身声学空腔有限元模型两部分。 其中,车身结构的有限元模型包括结构件的有限元模型和非结构件的有限元模型,非结构件的有限元模型就用集中质量来模拟。声学空腔的有限元模型用有限元流体的单元来模拟,包括乘员仓空腔,座椅和行李箱空腔三部分的有限元模型。图1表示了车身分析模型的结构关系。
声学单元的理想尺寸大约是每个波长不少于六个单元,实际上通常采用的声学单元的长度一般为0.1米左右,已经满足了有限元计算的频率范围。根据空气中的声速和噪声分析频率可以计算出声波的波长以及声学单元的理想长度,本文中所建立的模型取声学单元的长度为0.12米。另外,要求流体的单元尺寸要大于结构单元的尺寸,以保证流体模型界面上的节点都能够与结构单元的节点相耦合。
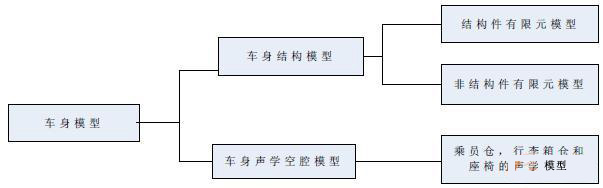
图1 车身有限元分析的结构图
3 分析方法
应用MSC Nastran软件,先进行结构和空腔的模态分析,然后用模态叠加法进行模态响应分析。
3.1 空腔和结构的模态分析
汽车车室构成封闭系统,形成一个声学系统。将车室空腔容积离散化为有限元单元,则空腔方程可以写成以下的矩阵形式:
![]()
式中:Mff和Kff就是车室空腔的声学质量矩阵和声学刚度矩阵;{Ff}为各单元表面传给流体的广义力向量;{p}为各节点的声压向量。
车身的有限元方程式可以写为:
![]()
式中:[Mss]和[Kss]就是车室空腔的声学质量矩阵和声学刚度矩阵;{Fs}为施加于结构上的外向力;{u}为结构位移向量。
3.2 进行声腔—结构的耦合分析
如果把车身结构视为弹性体,那么车身壁板的振动会通过临近的空气压迫车室内的空气,使之产生不同的声压,而车室声压的变化又会激励车身壁板的振动,使车室成为结构-流体(空气)相互作用的耦合系统,这个耦合系统的有限元方程可以写为:
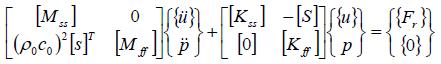
式中:[S]是由声学广义力{Fr}向量得到的车室结构-声学耦合矩阵;ρ0为空气密度;C0是声波在媒质中传播的速度。
3.3 把空腔压力转化为声压值
最后测试为测量点的空气压力转化为测试点处的声压值:
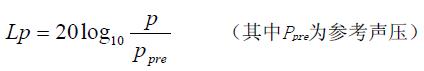
4 结果及优化
根据计算结果,发现有超过分析目标值的峰值出现。针对出现峰值的不同情况,分别采用模态参与因子和壁板贡献量分析方法,找出贡献比较大的部件和壁板,然后对这些零件进行改进。
图2分别是副车架右后安装点和后减振器右安装点激励下驾驶员右耳侧的响应结果,蓝色曲线是初始的设计状态的结果,红色曲线是优化后的结果。根据优化前后的结果比较,噪声响应的最大峰值都有5个dB的降低,一些峰值还消失了。经过优化,驾驶员耳侧的NVH特性得到很大改善。
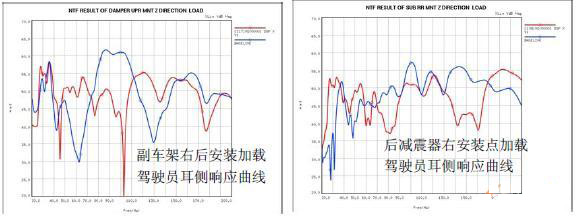
图2 在不同工况下优化前后的结构比较
5 结论
根据噪声传递函数分析及其优化分析可以发现,用有限元法进行车身的噪声传递函数分析是提高车身的NVH性能的有效方法。